Part1 前言

P5649 Sone1 是一个神奇的题，用 $25$ 个字概括：

链加链赋值，最值与求和，子树加赋值，最值与求和，换根换父亲。

可以认为是一道解法很多的开放题。

Part2 重工业理论与实现细节

$\text{LCT}$ 的原理是使用 splay 维护实路径，这样可以实现平摊 $O(\log n)$ 实现链修改，链查询。

为了对虚儿子进行维护，我们应当新开一个 splay 维护虚儿子，编号为 $x+n$。

每一个父亲记录其虚儿子 splay 的根节点，注意，只有 isroot(x)，$x+n$ 才有意义。

事实上，实路径和虚子树的 splay 可以共用，在实路径 splay 时，需要将原来的根节点从虚子树中删除，再将新的根节点插入，复杂度瓶颈就在此处。

这样来说，如果把虚子树根看作中儿子，这就是三度化的 $\text{SATT}$。

但我还是看不懂 $\text{SATT}$，由于找前驱后继无法平摊，所以时间为 $O(\log^2n)$。

用 $\text{SLT,splay-leafy-tree}$ 来维护虚儿子可以做到 $O(\log_2n)$ 的 access。

但这样无法共用 splay，码长要翻一倍，这也称为 $\text{AAAT}$。

重工业还有一个特点，把 tag 看作一次函数，将 dat 打包，省去了 addtag 和 pushdown 的分类讨论，进一步减小码量，当然这个也可以单纯地用矩阵乘法来理解。

具体实现要记录两个标记，表示链上修改和链外（虚子树）修改，还要记录三个数据，表示链上和，链外（虚子树）和，还有自己的值。

贴上评测链接。

Part3 从 $\text{AAAT}$ 理论到 $\text{SATT}$

显然，大多数大佬能看懂论文哥的文章。

但实现部分我是观察 AC 代码才理解的。

如果你只想学一种动态树而不愿意多做研究，那么只需要能理解 $\text{AAAT}$ 理论，那么你也能看懂 $\text{SATT}$ 的实现过程。

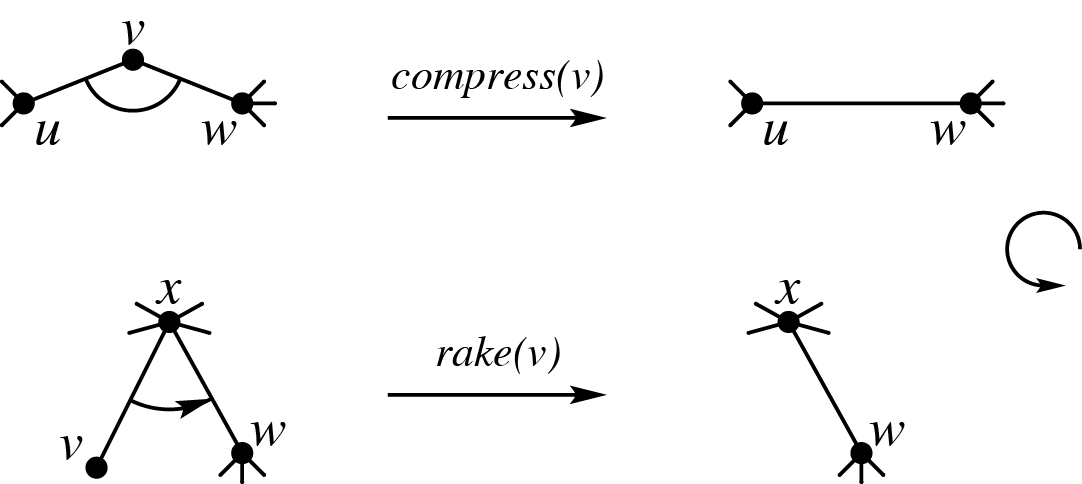
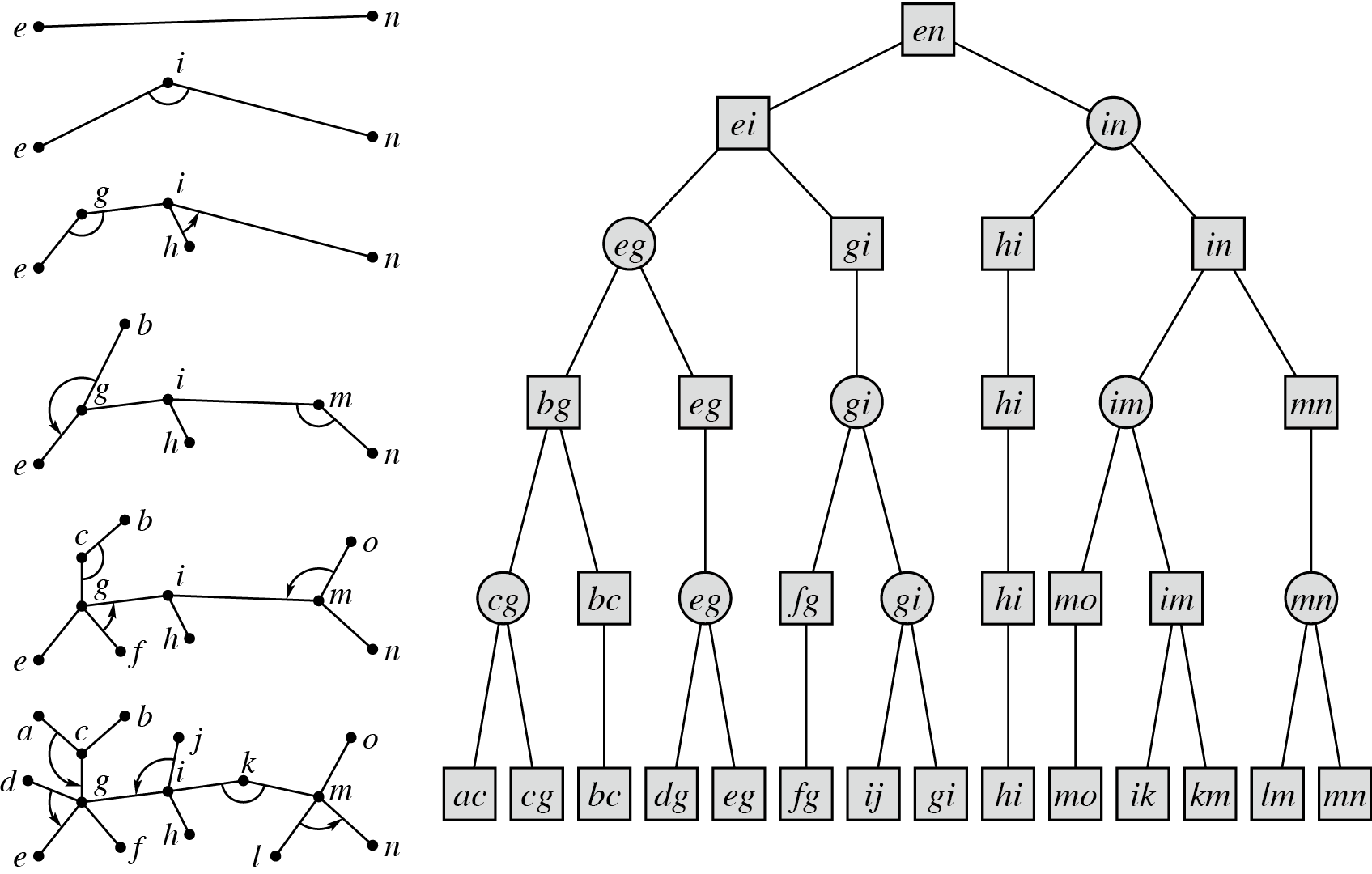
但在读下文前，请先将论文哥的文章先读三遍，可以大致理解一下 $\text{top-cluster}$ 理论。

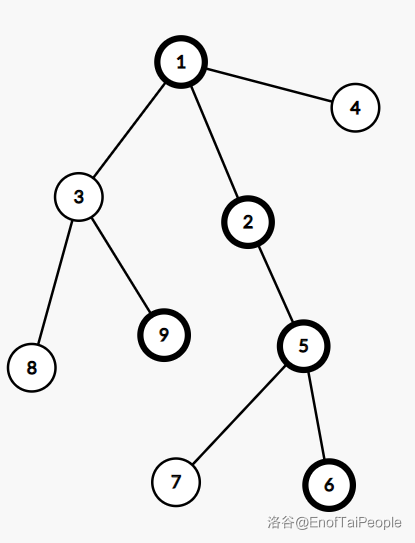
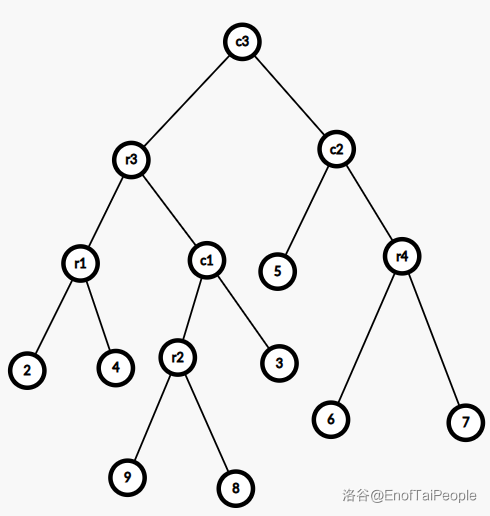
上图是一棵树，加粗的点表示实儿子，这棵树所对应的 $\text{SATT}$ 如下图：

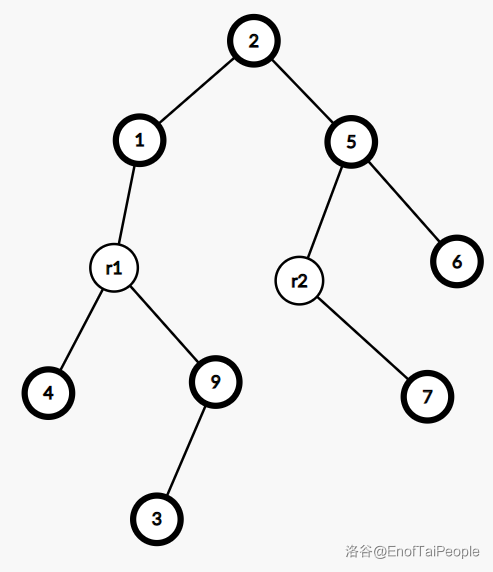
其中的 $r1,r2$ 表示 $\text{rake node}$，其余表示 $\text{compress node}$。

可以粗略理解为 $\text{compress node}$ 维护实链，$\text{rake node}$ 维护虚儿子。

但这里 $\text{rake node}$ 并没有和上方的 $\text{compress node}$ 失去联系，而成为了$\text{compress node}$ 的中儿子。

$\text{compress node}$ 在 pushdown 时需要加给子树的标记会传给中儿子。

$\text{rake node}$ 在 pushdown 时会给子树的两个标记都加上自己的标记。

注意 $\text{rake node}$ 只有一个标记，所以接受标记时也只有一个标记会用到。

可以简单理解成 $\text{rake node}$ 是维护虚子树的 $\text{SLT}$，但如果只有一个虚儿子，唯一的 $\text{rake node}$ 也会只有一个儿子。

任何时刻 $\text{rake node}$ 都不会有中儿子。

access 时只需要一次全局 pushdown，因为任何一个节点都可以一次经过 $\text{compress node}$ 和 $\text{rake node}$ 到达根簇。

遍历时只需要从根簇出发，遍历左右儿子和中儿子即可。

这样可以整体看作一棵大 splay，access 时间复杂度为均摊 $O(\log n)$。

由于只需要一次全局 pushdown，只有一棵树，常数相较 $\text{AAAT,LCT-ETT}$ 十分优秀，码量也很小。

Part4 其他做法

上面提到了两种做法是 $O(q\log^2n)$ 的：虚子树 $\text{LCT}$，$\text{LCT-ETT}$。

也有两种是 $O(q\log n)$ 的：$\text{AAAT}$ 和 $\text{SATT}$。

你会发现，它们都是基于 $\text{LCT}$ 的，所以时间复杂度都是均摊的。

假如你想要严格复杂度，甚至可持久化。

我们先考虑只要非暴力就行的方法。

注意：以下部分纯口胡，有错误可以直接指出。

• 每次打通最多增加 $O(\log n)$ 势能，所以可以每 $K$ 次操作重构，注意这里需要重链剖分建全局平衡二叉树。
• 于是重构复杂度为 $O(\dfrac{qn}K)$。
• 每次操作最多使用 $O(K\log n)$ 势能。
• 总复杂度为 $O(qK\log n+\dfrac{qn}K)$。
• 平衡一下取 $K=\sqrt{n\log n}$，总时间 $O(q\sqrt{n\log n})$。

否则你就不能使用势能了，而需要保证操作结束后保持严格重剖，具体地你需要将轻边抖落，重边连上，同时使用重量平衡树，注意这里使用 treap 做到期望复杂度会相对好写。

当然这个算法是暂时被我认为是考场不可写作的，注意 $\text{LCT}$ 和 $\text{SATT}$ 并不是。

Part5 后记

这道题可以被称作 $\text{Top Tree}$ 的简单应用，事实上静态时的 $\log$ 划分结构也是 $\text{Top Tree}$ 的良好性质，详见此文，于是这道题就真的成为 $\text{Top Tree}$ 的简单应用了。

Part1 前言

题意需要我们维护一棵静态树，$\text{rake}$ 和 $\text{compress}$ 都需要通过调用函数实现，查询到节点 $x$ 距离不超过 $d$ 的边集信息，且每次查询只能进行一次信息合并，$n\le2\times10^5,q\le10^6$。

它们是树收缩（$\text{tree contraction}$）的两个基本操作，$\text{rake}$ 消除一个度为 1 的点，$\text{compress}$ 消除一个度为 2 的点，此外这些操作会把两条边替换为一条边，收缩过程中，簇的合并结构形成了一个树：

Part2 $\text{Top Tree}$ 维护边集的静态构建

这道题的本质是 $\text{Top Tree}$ 上换根 dp，为了方便转移和查询，我们需要将 $\text{Top Tree}$ $\text{leafy}$ 化，使得每一条边所对应节点都是叶子，然后参照全局平衡二叉树的建立方式，注意节点 $1$ 没有父边，所以要忽略掉。

上图是一棵树，加粗的点表示重儿子，它所对应的 $\text{leafy-top-tree}$ 如下图：

其中 $r1\sim r4$ 表示 $\text{rake-node}$，$c1\sim c3$ 表示 $\text{compress-node}$，容易发现，它是一棵二叉树，有 $2n-3$ 个节点。

Part3 对簇内信息的记录

簇其实就是连通的边集，并且有两个端点，上图的 $\text{Top Tree}$ 中，每一个节点都表示了一个簇。

如何维护簇内信息？

记 $g(x,0/1,k)$ 表示到左右端点距离为 $k$ 以内的边集信息。

对于一个 $\text{rake-node}$，左端点的信息就是两颗子树对应距离 $\text{rake}$ 得到的结果，由于建树时默认重儿子在左子树，所以右端点会继承左子树的右端点，自然也会继承左子树的右端点邻域信息。

对于每一个节点，维护一个 $len$，表示簇的左右端点距离，这样继承之后会将右儿子的 $k-len$ 邻域信息并进来：

ln[x]=ln[ls],U[x]=U[ls],V[x]=V[ls];
for(i=0;i<=rz[x];++i){
    g[x][0][i]=R(G(ls,0,i),G(rs,0,i));
    g[x][1][i]=R(G(ls,1,i),G(rs,0,i-ln[x]));
}

对于一个 $\text{compress-node}$，左端点是左儿子的左端点，右端点是右儿子的右端点，合并时 $len$ 会相加，同样在处理左/右端点信息时取的是右/左儿子的 $k-len$ 邻域信息：

ln[x]=ln[ls]+ln[rs],U[x]=U[ls],V[x]=V[rs];
for(i=0;i<=rz[x];++i){
    g[x][0][i]=C(G(ls,0,i),G(rs,0,i-ln[ls]));
    g[x][1][i]=C(G(ls,1,i-ln[rs]),G(rs,1,i));
}

由于每一个节点只会保留边数的信息，而此树具有全局平衡的性质，所以时空复杂度 $O(n\log_2n)$，这样就可以通过 $u=1$ 和 $n\le2000$ 的测试点了，具体地，可以对于每一个需要的根节点建一棵树，由于根节点必定是根簇的左端点，所以可以直接查询簇内信息，可以得到 $30pts$，时空复杂度 $O(rn\log_2n)$，$r$ 表示查询的不同节点个数。

Part4 对簇外信息的记录

发现对于一个节点，如果不是根簇端点，可能会很尴尬：从叶子往上跳，跳多了得到的信息就超了，跳少了信息又不完全，我们无法做到让查询的信息总在一个簇内与簇的某一端点完全相邻，于是需要记录簇外的信息。

记 $h(x,0/1,k)$ 表示 $x$ 的簇外到左/右节点距离为 $k$ 以内的邻域信息。

无论是哪一个节点，它的簇外信息都有两部分组成：父亲的簇外信息和兄弟的簇内信息，这方面不难推导，依旧只需要对于两种类型的节点分类讨论就可以了：

if(tp[x]){
    h[ls][0].resize(rz[x]+1);
    h[ls][1]=h[rs][0]=h[ls][0];
    h[rs][1]={emptyinfo};
    for(i=0;i<=rz[x];++i)
        h[ls][1][i]=H(x,1,i);
    for(i=0;i<=rz[x];++i){
        h[ls][0][i]=R(G(rs,0,i),H(x,0,i));
        h[rs][0][i]=R(C(G(ls,0,i),H(ls,1,i-ln[ls])),H(x,0,i));
    }
}else{
    h[ls][0].resize(rz[x]+1);
    h[rs][0]=h[ls][1]=h[rs][1]=h[ls][0];
    for(i=0;i<=rz[x];++i){
        h[ls][0][i]=H(x,0,i);
        h[rs][1][i]=H(x,1,i);
        h[ls][1][i]=C(H(x,1,i-ln[rs]),G(rs,0,i));
        h[rs][0][i]=C(H(x,0,i-ln[ls]),G(ls,1,i));
    }
}

大家可能发现了，对于每一个节点的簇外信息，我们都将其保留到了父亲的大小，这样可以方便查询。

具体地，从查询节点开始跳，直到父亲的簇大小超过 $d$ 为止，这样当前的簇内信息必定被完全包含，簇外信息也必定经过了预处理，可以通过两次 $\text{compress}$ 得到答案。

容易发现，这一部分必定会完全包含簇内信息，所以在预处理时将 $h(x,0,k)$ 与 $g(x,0,sz_x)$ 合并，就能保证查询时只需要一次 $\text{compress}$ 了，符合题意要求，时空复杂度 $O(n\log_2n)$。

Part5 代码效率说明

首先，这是我的第一次提交记录，也推荐大家参考，因为没有删注释，但是只有 $97$ 分，因为交完之后，我发现在本地纯随机造树就卡成了 too many MR,MC operations in init()，然后就莫名其妙地 Hack 成功了，后来发现这是被卡常了，微调了一下建树过程，就通过了，或许是出题人并不想卡人？反正目前是最优最短解，指不定哪一天就被人挤下去了。

然而，这样的做法又被我自己 Hack 掉了，原因是，当数据为一棵完全二叉树时，高度会达到 $60$，或许在时间上没有问题，但函数调用次数会大大增加，超过了 $3\times10^7$，所以需要进一步卡常，具体地，在 dp 时不需要处理到边集大小，只需要处理到直径就可以了。

Part6 后记

不知道自己想干什么，学一道题目花了一个星期，或许这是我联赛之前的最后一次任性吧。但这道题真的十分有教育意义，将树上问题在链和子树的基础上，又向全新的“邻域”问题发展，也让我了解到了 $\text{Top Tree}$ 的更多功能。

Part1-Improved Dinic

ID（Improved Dinic) 算法是一种求最大流的高效算法，在随机图上复杂度为 $O(km)$，其中 $k$ 是一个较小的常数，一般在 $10$ 左右。缺点也很明显，加边离线，复杂度上限未知（可以理解为上限是 $O(kn^2m)$，但卡到 $O(nm)$ 都不容易做到）。

ID 算法原理就是，对 Dinic 算法进行很多优化，最后不仅代码较短，效率也很高，值得一提的是，即使是小规模数据，他也能跑得比一般算法快。

具体优化如下：

1. 当前弧（允许弧）优化；
2. 分段加边优化；
3. 先正后反（贪心初始流）优化；
4. gap 优化。

当前弧（允许弧）优化大家都懂，分段加边优化是为了防止边权差异过大，因为 Dinic 算法只有在边权差异大时会跑得较慢。

贪心初始流是采用了二分图增广路算法的贪心初始匹配思想，先不连反边是为了不然反边影响初始效率，gap 优化可以参照 ISAP，AC 记录。

Part2-LCT-Dinic

这是一个最坏复杂度为 $O(nm\log n)$ 的最大流算法。

把 ID 卡慢很简单，$k$ 可以被卡到 $\frac n3$ 左右，虽然通过此题的数据范围绰绰有余。

我们需要对 Dinic 的增广过程进行研究，考虑其之所以单次增广最坏为 $O(nm)$ 是因为每一条增广路最多有 $n$ 个点，由于可能每一条路有且仅有一条边满流，所以最多会增广 $m$ 次。

发现一条边在一条增广路上如果没有满流，就还会继续扫到，这样对效率的影响极大，于是可以用数据结构来维护连边，断（零）边，链减（得到的流量），使用可爱的 LCT 十分合适，于是就这样愉快地决定啦！

由于单次增广每一条边最多只会加入一次，减少一次，每一次加入减少的复杂度都是平摊 $O(\log n)$ 的，于是总复杂度为 $O(nm\log n)$。

加上 ID 的优化三（贪心初始流）就可以通过 luogu 数据了，并且速度比 ID 快一倍。

但是，在 UOJ 上会 TLE。

Part3-总结

其实 HLPP 的优势局限于本题的数据范围，再稠密点常数没有 MPM 小，再稀疏点就不如 LCT-Dinic。

以上 ID 的代码能通过 Luogu、LOJ、UOJ 的数据，但 LCT-Dinic 即使分段连边也通不过 UOJ 的第三十个测试点，而该点 ID 却能在 $1ms$ 内通过，所以特殊构图能卡 LCT-Dinic，毕竟 LCT 常数大，且每次都有 $\log$，并且分段连边时答案变得飞快，根本没有一条一条 $\log$ 增广的时间。

事实上，我还没见过有人在建模题上卡 Dinic，这就当整活图一乐了。